On considère deux fonction f et g définies sur I.
Propriété : Les solutions de l'équation f(x)=k sont les abscisses des points de la courbe de f dont l'ordonné est k.
Propriété : Les solutions de l'équation f(x)=g(x) sont les abscisses des points d'intersection des courbes de f et de g.
Propriété : Les solutions de l'équation f(x) < k sont les abscisses des points de la courbe de f dont l'ordonné est strictement inférieur à k.
Propriété : Les solutions de l'équation f(x)< g(x) sont les abscisses des points de la courbe de f situé au dessous de la courbe de g .
Important : Attention aux sens des crochets des intervalles.
Il faut parfois donner des valeurs approchées.
Il faut parfois donner des valeurs approchées.
Méthode :
Pour résoudre graphiquement une équation ou une inéquation :
tracer la droite y=k
repérer les abscisses des points d'intersections de la courbe et de la droite
On peut utiliser un stabilo pour repérer les points de la courbe au dessus ou au dessous de la droite
Il reste à lire les intervalles correspondant à ces points sur l'axe des abscisses.
Attention aux crochets
Pour résoudre graphiquement une équation ou une inéquation :
tracer la droite y=k
repérer les abscisses des points d'intersections de la courbe et de la droite
On peut utiliser un stabilo pour repérer les points de la courbe au dessus ou au dessous de la droite
Il reste à lire les intervalles correspondant à ces points sur l'axe des abscisses.
Attention aux crochets
Exercice 1 Construire la courbe représentative de la fonction sur l'intervalle [-3;4]
a) Résoudre f(x)=2
b) Résoudre f(x) \leq 1
c) Résoudre f(x) \geq 1
a) Résoudre f(x)=2
b) Résoudre f(x) \leq 1
c) Résoudre f(x) \geq 1
Exercice 2 .PNG)
a) Résoudre f(x)=2
b) Résoudre f(x) \leq 1
.PNG)
a) Résoudre f(x)=2
b) Résoudre f(x) \leq 1
Exercice 3 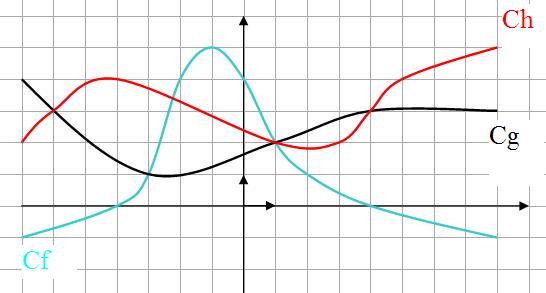
a) résoudre f(x) < g(x)
b) résoudre f(x) \leq h(x)
c) résoudre g(x) \geq h(x)
a) résoudre f(x) < g(x)
b) résoudre f(x) \leq h(x)
c) résoudre g(x) \geq h(x)