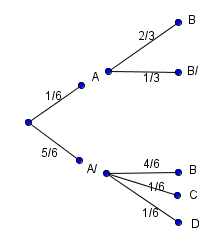
On lance un dé équilibré. Si l'on obtient 1, on tire au hasard un jeton dans une urne U1 qui contient 2 jetons bleus et un jeton blanc. Si l'on obtient un autre chiffre que 1, on tire au hasard un jeton dans une urne U2 qui contient 4 jetons bleus, 1 blanc et un rouge.

Les événements A "Obtenir 1" et B"Tirer un jeton bleu" sont-ils des événements indépendants ?

1-On peut s'aider d'un arbre de probabilité.

2-Chercher la définition de deux événements indépendants.

On a P(\(A \cap B\))=P(A)*P(B)=\(\frac{1}{{6}}\)*\(\frac{2}{{3}}\)=\(\frac{1}{{9}}\)

P(A)=\(\frac{1}{{6}}\)

P(B)=P(\( A \cap B\))+P(\(\overline{A}\)\( \cap B\))=\(\frac{1}{9}\)+\(\frac{5}{6}\)*\(\frac{4}{6}\)=\(\frac{2}{3}\)

Donc P(A)*P(B)=\(\frac{1}{{6}}\)*\(\frac{2}{{3}}\)=\(\frac{1}{{9}}\)

Comme P(\(A \cap B\))=P(A)*P(B) alors les événements Aet B sont deux événements indépendants.

1- Dire que deux événements sont indépendants signifie que l'on a P(\( A \cap B\))=P(A)*P(B)

2-Dire que deux événements sont indépendants signifie que la probabilité de l'un n'est pas influencée par la réalisation ou non de l'autre. 

C'est à dire:

-\(\mathrm{P}_A(B)\)=\(\mathrm{P}_\overline{A}(B)\)=P(B)

-\(\mathrm{P}_B(A)\)=\(\mathrm{P}_\overline{B}(A)\)=P(A)

3- Si A et B sont deux événements indépendants, alors \(\overline{A}\) et B sont aussi indépendants.