Le plan complexe est rapporté à un repère orthonormé $(O;\vec{u}; \vec{v})$. À tout point $M$ d'affixe $z$
du plan, on associe le point $M'$ d'affixe $z'$ définie par:
\[z' = z^2 + 4z + 3.\]
Un point $M$ est dit invariant lorsqu'il est confondu avec le point $M'$ associé.
Démontrer qu'il existe deux points invariants. Donner l'affixe de chacun de ces points
sous forme algébrique, puis sous forme exponentielle.
$M(z)$ est invariant si $M' = M \iff z' = z \iff z^2 + 4z + 3 = z \iff z^2 + 3z + 3 = 0$.
$M(z)$ est invariant si $M' = M \iff z' = z \iff z^2 + 4z + 3 = z \iff z^2 + 3z + 3 = 0$.
$\Delta = 3^2 - 4 \times 3 = 9 - 12 = - 3 = \left(\text{i}\sqrt{3}\right)^2$.
Cette équation a deux solutions :
$z_1 = \dfrac{ - 3 + \text{i}\sqrt{3}}{2}$ et $z_2 = \dfrac{ - 3 - \text{i}\sqrt{3}}{2}$.
On a $\left|z_1\right|^2 = \left(- \frac{3}{2}\right)^2 + \left(\frac{\sqrt{3}}{2} \right)^2 = \frac{9}{4} + \frac{3}{4} = 3 \Rightarrow \left|z_1\right| = \sqrt{3}$.
Le même calcul donne $\left|z_2\right| = \sqrt{3}$.
On a donc $z_1 = \dfrac{ - 3 + \text{i}\sqrt{3}}{2} = \sqrt{3}\left(- \dfrac{\sqrt{3}}{2} + \text{i}\dfrac{1}{2}\right) = \sqrt{3}\left(\cos \frac{5\pi}{6} + \text{i}\sin \frac{5\pi}{6}\right) = \sqrt{3}\text{e}^{\text{i}\frac{5\pi}{6}}$.
On trouve de la même façon que $z_2 = \sqrt{3}\text{e}^{-\text{i}\frac{5\pi}{6}}$.
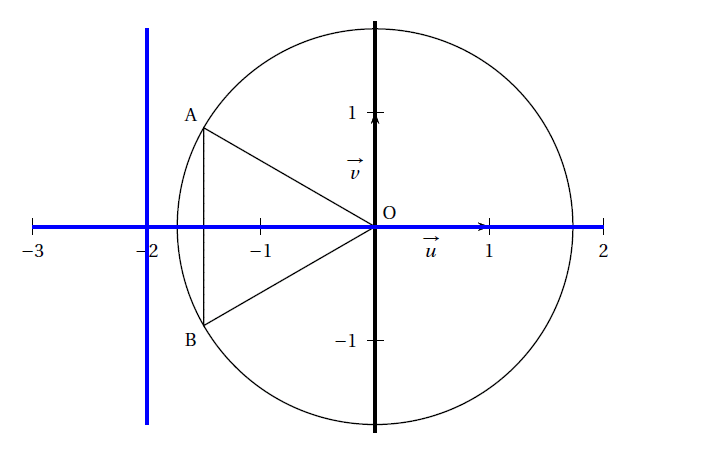
Soit A le point d'affixe $\dfrac{- 3 - \text{i}\sqrt{3}}{2}$ et B le point d'affixe
$\dfrac{- 3 + \text{i}\sqrt{3}}{2}$.
On a $z_{\text{A}} = z_2$, donc $\left|z_{\text{A}} \right| = \text{OA} = \left|z_2 \right| = \sqrt{3}$.
De même $z_{\text{B}} = z_1$, donc $\left|z_{\text{B}} \right| = \text{OB} = \left|z_1 \right| = \sqrt{3}$.
Enfin $\text{AB} = \left|z_{\text{B}} - z_{\text{A}} \right| = \left|\dfrac{- 3 + \text{i}\sqrt{3}}{2} - \left(\dfrac{- 3 - \text{i}\sqrt{3}}{2} \right) \right| = \left|\text{i}\sqrt{3} \right| = \sqrt{3}$.
On résout une équation du second degré telle que \[ az^2 + bz + c = 0 \] en calculant le discriminant \[\Delta = b^2-4ac.\] $\Delta$ sera inférieur à $0$ donc les abscisses des points pour lesquelles $M$ = $M'$ sont $x_1$ et $x_2$ tels que
$x_1$ = $\dfrac{- b - \text{i}\sqrt{\Delta}}{2a}$ et $x_2$ = $\dfrac{- b + \text{i}\sqrt{\Delta}}{2a}$
Déterminer l'ensemble $\mathcal{E}$ des points $M$ d'affixe $z = x + \text{i}y$ où $x$ et $y$ sont réels, tels que le point $M'$ associé soit sur l'axe des réels.
$M'$ est sur l'axe des réels si $y' = 0$.
$M'$ est sur l'axe des réels si $y' = 0$.
Or on sait que l'affixe du point $M$ est :
$z^2 + 4z + 3 = (x + \text{i}y)^2 + 4(x + \text{i}y) + 3 = x^2 - y^2 + 2\text{i}xy + 4x + 4\text{i}y + 3 = x^2 - y^2 + 3 + \text{i}(2xy + 4y)$.
On a donc $y' = 0 \iff 2xy + 4y = 0 \iff 2y(x + 2) = 0 \iff \left\{\begin{array}{l c l}
y&=&0\\
x + 2&=&0
\end{array}\right. \iff \left\{\begin{array}{l c l}
y&=&0\\
x &=&- 2
\end{array}\right.$
Conclusion : l'ensemble $\mathcal{E}$ est constitué des points d'ordonnée nulle donc de l'axe des abscisses et des points de la droite verticale dont une équation est $x = - 2$ (droites en bleu).
Dans le plan complexe, représenter les points A et B ainsi que l'ensemble $\mathcal{E}$.
Utiliser les ensemble de points
En utilisant module et argument :
L'ensemble des points M d'affixe Z tel que:
| $|Z-Z_A|=R$ | Le cercle de centre A et rayon R |
| $|Z-Z_A|=|Z-Z_B|$ | La médiatrice du segment [AB] |
| $Z-Z_A=Re^{i\theta}$ avec $\Theta \in [0;2\pi]$ | Le cercle de centre A et rayon R |
| $Z-Z_A=Re^{i\theta}$ avec $\Theta \in [0;\pi]$ | Un demi cercle de centre A et rayon R |
| $Z=Re^{i\theta}$ avec$ R \in \mathbb{R} $ | Une droite passant par l'origine |
| $Z-Z_A=Re^{i\theta}$ avec $ R \in \mathbb{R}_+$ | Une demi droite d'origine A |
| $Z-Z_A=Re^{i\theta}$ avec $ R \in [0;1]$ | Un segment [AB] |
En utilisant la forme algébrique :
L'ensemble des points M d'affixe $Z=a+ib$ tel que:
| $a=0$ | l'axe des ordonnée |
| $b=0$ | l'axe des abscisse |
| $a=k$ ou k est une constante |
Une droite verticale d'équation $x=k$ |
| $b=pa+m$ | La droite d'équation $y=px+m$ |
| $(a-x_A)²+(b+y_A)²=R²$ | Le cercle de centre A et rayon R |
Exemple d'utilisation:
Soit A(1+i) et 0 l'origine du repére.
Determinons l'image de la droite (OA) par la transformation $f(z)={1 \over {\overline{z}}}$
Ces tableaux se lisent dans les deux sens:
Soit M(a+ib) un point de (OA), on à alors a=b.
l'affixe de $M'$ est $Z_{M'}={{1} \over {a-ib}}$
$Z_{M'} = {{a+ib} \over {\sqrt{a^2+b^2}}}$
comme $a=b$
M' est sur la droite d'équation $y=x$
(On dit que la droite (OA) est un ensemble globalement invariant )
Determinons l'image du cercle $C$ de centre 0 rayon 2 par la transformation $f(z)={1 \over {\overline{z}}}$
Soit M un point de C, $Z_M=2e^{i\theta}$ avec $\theta \in [0;2\pi]$
On à alors $Z_{M'}={1\over2}e^{i\theta}$ avec $\theta \in [0;2\pi]$
M' est sur le cercle de centre 0 et de rayon $1\over2$
- Soit A le point d'affixe $\dfrac{- 3 - \text{i}\sqrt{3}}{2}$ et B le point d'affixe $\dfrac{- 3 + \text{i}\sqrt{3}}{2}$.
Montrer que OAB est un triangle équilatéral.
- Représentez l'ensemble $\mathcal{E}$ dans le plan complexe
Calculer la distance OA, la distance OB et la distance AB
On a donc $\text{OA} = \text{OB} = \text{AB} = \sqrt{3}$ : le triangle OAB est un triangle équilatéral.
Déterminer l'ensemble $\mathcal{E}$ des points $M$ d'affixe $z = x + \text{i}y$ où $x$ et $y$ sont réels, tels que le point $M'$ associé soit sur l'axe des réels.
Soit $M(x~;~y)$ et $M'(x'~;~y')$ son point associé.
$M'$ est sur l'axe des réels si $y' = 0$.
Or on sait que l'affixe du point $M$ est :
$z^2 + 4z + 3 = (x + \text{i}y)^2 + 4(x + \text{i}y) + 3 = x^2 - y^2 + 2\text{i}xy + 4x + 4\text{i}y + 3 = x^2 - y^2 + 3 + \text{i}(2xy + 4y)$.
On a donc $y' = 0 \iff 2xy + 4y = 0 \iff 2y(x + 2) = 0 \iff \left\{\begin{array}{l c l}
y&=&0\\
x + 2&=&0
\end{array}\right. \iff \left\{\begin{array}{l c l}
y&=&0\\
x &=&- 2
\end{array}\right.$
Démontrer une propriété de géométrie
I) Démontrer en maths
Il faut bien distinguer deux choses :
- Faire une constatation à partir d’une figure ou à partir de calcul.
- Démontrer en utilisant une propriété.
En mathématiques, on demande presque toujours de démontrer les résultats. La figure ou les exemples sont là uniquement pour nous aider à faire cette démonstration.
A) Règles de base…
1 : Un énoncé mathématique est soit vrai, soit faux.
2 : Des exemples qui vérifient un énoncé ne suffisent pas pour prouver qu’un énoncé est vrai.
3 : Un exemple qui ne vérifie pas un énoncé (appelé contre-exemple) suffit pour prouver que l’énoncé est faux.
→ Plusieurs exemples ne suffissent pas pour montrer qu’une propriété est vraie mais un seul contre-exemple suffit pour montrer qu’une propriété est fausse !
4 : Une constatation ou une mesure ne suffit pas à prouver qu’un énoncé de géométrie est vrai.
B) Comment démontrer ?
Une démonstration s’écrit en trois étapes :
Etape 1 : Je sais … (hypothèses)
Les hypothèses se trouvent dans l’énoncé de l’exercice, les codes d’une figure géométrique, les questions précédentes.
Etape 2 : (conditions et conséquences)
On utilise une propriété ou une définition.
Etape 3 : (conséquences)
On conclut.
II) Exemple de démonstrations
A) Rappels
Ce qui est essentiel, c’est de faire la liaison entre géométrie et nombres complexes !!
- Affixe du vecteur $\vec{AB}$ : $Z_{\vec{AB}} = Z_B-Z_A$
- Module $\iff$ distance : $|z|=\sqrt{a^{2}+b^{2}}$
- Argument $\iff$ angle : $arg(\vec{AB};\vec{AC})$ $=$ $\frac{z_C-z_A}{z_B-z_A}$
B) Utilisations des modules :
Montrer que $|z_M-z_A|=2$ permet de montrer que le point M est sur le cercle de centre A et de rayon 2.
Montrer que $|z_M-z_A|=|z_M-z_B|$ permet de montrer que le point M est sur la médiatrice du segment $[AB]$
Montrer que deux diagonales d'un parallélogramme sont de même mesure permet de montrer que c'est un rectangle.
Montrer que deux cotés consécutif d'un parallélogramme sont de même mesure permet de montrer que c'est un losange.
Montrer qu'un triangle posséde deux cotés de même longueur, c'est montrer qu'il est isocèle.
Montrer qu'un triangle posséde trois cotés de même longueur, c'est montrer qu'il est équilatérale.
C) Utilisation des vecteurs :
Montrer que deux vecteurs sont égaux, c'est montrer qu'on à un parallélogramme.
Montrer qu'il existe un réel $k$ tel que $\vec{AB}=k\vec{CD}$ c'est montrer que les droites $(AB)$ et $(BC)$ sont paralléles.
Montrer qu'il existe un réel $k$ tel que $\vec{AB}=k\vec{CB}$ c'est montrer que les points $A,B,C$ sont alignés.
D) Utilisation de l'argument :
Montrer qu'un triangle posséde deux angles égaux, c'est montrer qu'il est isocèle.
Montrer qu'un triangle posséde trois angles égaux , c'est montrer qu'il est équilatérale.
Montrer qu'un triangle posséde un angle égal à $\pi\over 2$, c'est montrer qu'il est rectangle.
Montrer qu'un angle est nul peut permettre de montrer que des points sont alignés, des droites sont paralléles.
...