Exercice 1 (5pts)
Commun à tous les candidats
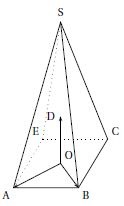
Dans l'espace, on considère une pyramide SABCE à base carrée ABCE de centre O. Soit D le point de l'espace tel que $\left(\text{O}~;~ \vec{\text{OA}},~ \vec{\text{OB}}, \vec{\text{OD}}\right)$ soit un repère orthonormé. Le point S a pour coordonnées (0 ; 0 ; 3) dans ce repère.
Partie A
1. Soit U le point de la droite (SB) de côté 1. Construire le point U sur la figure jointe en annexe 1, (à rendre avec la copie).
Utilisez le théorème de Thalès pour construire le point $U$...
On peut utiliser ici le théorème de Thalès pour prouver que $\vec{BU} = \dfrac{1}{3}\vec{BS}$ et ainsi construire le point.
Pour cela considérons le triangle $SOB$.
Nous savons que $(DU)$ est parallèle à $(OB)$ car $D$ et $U$ partagent le même côté et $O$ et $B$ sont également de même côté. Nous savons également que $\dfrac{OD}{OS} = \dfrac{1}{3}$, là encore en raison du côté de $D$ et $S$. On en déduit, par application de l'antique théorème, que $\dfrac{BU}{BS} = \dfrac{OD}{OS} = \dfrac{1}{3}$.
2. Soit V le point d'intersection du plan (AEU) et de la droite (SC). Montrer que les droites (UV) et (BC) sont parallèles. Construire le point V sur la figure jointe en annexe 1, (à rendre avec la copie).
Utilisez le théorème du toit car les plans $(AUE)$ et $BCS)$ sont sécants en la droite $(UV)$...
Considérons les plans $(AUE)$ et $(BCS)$. Ces plans sont sécants en la droite $(UV)$. Or, $(BC)$, incluse dans $(BCS)$, est parallèle à $(AE)$, incluse dans $(AEU)$; puisque $ABCE$ est un carré.
Par application du théorème du toit, on en déduit que $(UV)$ est parallèle à $(BC)$. Cette dernière propriété permet de construire le point $V$.
Etudier la position relative de plans et de droites
I) Position relative de 2 plans :
1 - On regarde si les plans sont parallèles :
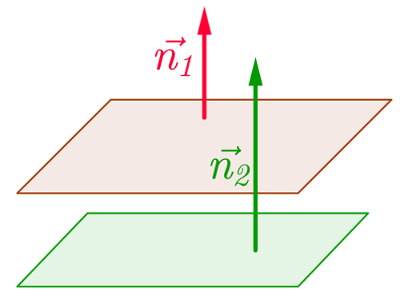
On regarde si un vecteur normal à un des plans est aussi normal à l'autre plan. Dans ce cas, $\vec{n_1}=k\vec{n_2}$. Avec $\vec{n_1}$ vecteur normal à l'un des plans et $\vec{n_2}$ vecteur normal à l'autre plan.
Si, dans l'égalité, on obtient un seul $k$ pour lequel:
xn1 = k xn2
yn1 = k yn2
zn1 = k zn2 ,alors les deux plans sont parallèles.
Si elle ne l'est pas, alors les plans sont sécants.
2 - On regarde si les plans sont orthogonaux :
On regarde si le vecter directeur à un plan est orthogonal au vecteur 
directeur du deuxième. Pour ce faire, on fait un produit scalaire :
Si $\vec{n_1}.\vec{n_2}=0$, alors les deux plans sont orthogonaux.
Dans le cas contraire, ils sont seulement sécants.
II) Position relative de 2 droites :
1 - On regarde si les droites sont parallèles :
On regarde si un vecteur directeur à une des droites est colinéaire à celui de l'autre droite.
Dans ce cas les droites sont parallèles (éventuellement sécantes )
2 - Si les droites ne sont pas parallèles :
On regarde si elles sont sécantes ou non coplannaires :
Avec les équations paramétriques, on cherche un point comun : Existe-t-il un paramêtre $k$ de la première équation et un paramêtre $k'$ de la seconde qui permet d'obtenir les même valeurs de x, y et z.
De plus si $\vec{n_1}.\vec{n_2}=0$, alors les deux droites sont orthogonales.
III) Position relative d'une droite et d'un plan :
1 - On choisit un vecteur directeur de la droite et un vecteur normal du plan :
S'ils sont colinéaires, le plan et la droite sont orthogonaux.
S'ils sont othogonaux, le plan et la droite sont parallèles.
2 - On cherche les points communs au plan et à la droite:
Il suffit de chercher s'il existe un paramêtre $k$ solutions des équations.
Si ce paramêtre est unique, il y à un point d'intersection.
Si toutes les valeurs sont solutions, la droite est incluse dans le plan .
Si il n'y a pas de solution, le plan et la droite sont strictement parallées.
3. Soit K le point de coordonnées $\left(\dfrac{5}{6}~;~ - \dfrac{1}{6}~;~0\right)$.
Montrer que K est le pied de la hauteur issue de U dans le trapèze AUVE.
Prouvez que $K$ appartient à $(AE)$...
Et montrer que $(KU)$ est perpendiculaire à $(AE)$...
Il nous faut prouver d'une part que $K$ appartient à $(AE)$ et d'autre part que $(KU)$ est perpendiculaire à $(AE)$.
On lit les coordonnées de A (1 ; 0 ; 0) et celles de E (0 ; -1 ; 0) et on calcule ainsi $\vec{AE}$ (-1 ; -1 ; 0). D'autre part on détermine $\vec{AK}$ ($\frac{-1}{6};{\frac{-1}{6}};{0}$).
On en déduit que $\vec{AK} = \dfrac{1}{6} \vec{AE}$, ce qui prouve que $K$ est un point de $[AE]$.
Déterminons les coordonnées de $U$. On a démontré dans la question 1 que $\vec{BU} = \dfrac{1}{3}\vec{BS}$, ce qui donne un système portant sur les coordonnées de $U$:
\[
\left \{
\begin{array}{lcl}
x_u-0 & = & \dfrac{1}{3}\left(0-0\right) \\
y_u-1 & = & \dfrac{1}{3}\left(0-1\right) \\
z_u & = & 1
\end{array}
\right .
\Longleftrightarrow
\left \{
\begin{array}{lcl}
x_u & = & 0 \\
y_u & = & \dfrac{2}{3}\\
z_u & = & 1
\end{array}
\right .
\]
On peut maintenant déterminer les coordonnées de $\vec{KU}$ (${-\frac{5}{6}} ; {\frac{5}{6}} ; {1}$.
On obtient ainsi, sachant que le repère est orthonormé: $\vec{KU} \cdot \vec{AE} = \dfrac{-5}{6} \times (-1) + \dfrac{5}{6} \times (-1) + 1 \times 0 = 0$, ce qui permet de conclure. Le point $K$ est bien le pied de la hauteur issue de $U$ dans le trapèze $AUVE$.
Démontrer une propriété de géométrie
I) Démontrer en maths
Il faut bien distinguer deux choses :
- Faire une constatation à partir d’une figure ou à partir de calcul.
- Démontrer en utilisant une propriété.
En mathématiques, on demande presque toujours de démontrer les résultats. La figure ou les exemples sont là uniquement pour nous aider à faire cette démonstration.
A) Règles de base…
1 : Un énoncé mathématique est soit vrai, soit faux.
2 : Des exemples qui vérifient un énoncé ne suffisent pas pour prouver qu’un énoncé est vrai.
3 : Un exemple qui ne vérifie pas un énoncé (appelé contre-exemple) suffit pour prouver que l’énoncé est faux.
→ Plusieurs exemples ne suffissent pas pour montrer qu’une propriété est vraie mais un seul contre-exemple suffit pour montrer qu’une propriété est fausse !
4 : Une constatation ou une mesure ne suffit pas à prouver qu’un énoncé de géométrie est vrai.
B) Comment démontrer ?
Une démonstration s’écrit en trois étapes :
Etape 1 : Je sais … (hypothèses)
Les hypothèses se trouvent dans l’énoncé de l’exercice, les codes d’une figure géométrique, les questions précédentes.
Etape 2 : (conditions et conséquences)
On utilise une propriété ou une définition.
Etape 3 : (conséquences)
On conclut.
II) Exemple de démonstrations
A) Rappels
Ce qui est essentiel, c’est de faire la liaison entre géométrie et nombres complexes !!
- Affixe du vecteur $\vec{AB}$ : $Z_{\vec{AB}} = Z_B-Z_A$
- Module $\iff$ distance : $|z|=\sqrt{a^{2}+b^{2}}$
- Argument $\iff$ angle : $arg(\vec{AB};\vec{AC})$ $=$ $\frac{z_C-z_A}{z_B-z_A}$
B) Utilisations des modules :
Montrer que $|z_M-z_A|=2$ permet de montrer que le point M est sur le cercle de centre A et de rayon 2.
Montrer que $|z_M-z_A|=|z_M-z_B|$ permet de montrer que le point M est sur la médiatrice du segment $[AB]$
Montrer que deux diagonales d'un parallélogramme sont de même mesure permet de montrer que c'est un rectangle.
Montrer que deux cotés consécutif d'un parallélogramme sont de même mesure permet de montrer que c'est un losange.
Montrer qu'un triangle posséde deux cotés de même longueur, c'est montrer qu'il est isocèle.
Montrer qu'un triangle posséde trois cotés de même longueur, c'est montrer qu'il est équilatérale.
C) Utilisation des vecteurs :
Montrer que deux vecteurs sont égaux, c'est montrer qu'on à un parallélogramme.
Montrer qu'il existe un réel $k$ tel que $\vec{AB}=k\vec{CD}$ c'est montrer que les droites $(AB)$ et $(BC)$ sont paralléles.
Montrer qu'il existe un réel $k$ tel que $\vec{AB}=k\vec{CB}$ c'est montrer que les points $A,B,C$ sont alignés.
D) Utilisation de l'argument :
Montrer qu'un triangle posséde deux angles égaux, c'est montrer qu'il est isocèle.
Montrer qu'un triangle posséde trois angles égaux , c'est montrer qu'il est équilatérale.
Montrer qu'un triangle posséde un angle égal à $\pi\over 2$, c'est montrer qu'il est rectangle.
Montrer qu'un angle est nul peut permettre de montrer que des points sont alignés, des droites sont paralléles.
...
Trouver une intersection
Il y a plusieurs types d'intersections:
Intersection de deux droites:
Si deux droites sont coplanaires et non parallèles alors leur intersection est un point.

Pour trouver les coordonnées du point d'intersection entre la droite D et la droite D', il faut se servir des équations paramétriques les deux droites et résoudre le système.
On cherche un couple de paramêtre $k$ et $k'$ tel que les valeurs de $x,y,z$ soient les même pour les deux droites.
Intersection d'une droite et d'un plan:
L'intersection entre une droite et un plan est un point
.png)
Pour trouver les coordonnées du point d'intersection entre la droite D et la plan P, il faut une équation cartésienne du plan et une équation paramétrique du plan. On remplace les x, y et z dans l'éqution du plan jusqu'à obtenir une valeur de t. On remplace cette valeur dans l'équation paramétrique de la droite D et on résout pour trouver des valeurs de x, y et z qui correspondent aux coordonnées du point d'intersection entre la droite D et la plan P.
Intersection de deux plans:
Si les deux plans ne sont pas parallèles, l'intersection entre deux plans est une droite.

Le système constitué par ces deux équations est un système d'équation cartésienne de droite.
On peut trouver un système d'équation paramètrique de la droite en posant $x=k$ ou $y=k$ ou ...
Remarque : Si un point appartient aux deux plans, il appartient à la droite d'intersection, et deux points définissent une droite.
Intersection d'un plan et d'une sphère:
L'intersection entre un plan et une sphère est un cercle.

Remarque : Le centre du cercle, celui de la sphère et un point du cercle forment un triangle rectangle, penser à Pythagore
Remarque : La distance entre le centre de la sphère et le plan donne la nature de l'intersection (vide, point ou cercle )
Partie B
Dans cette partie, on admet que l'aire du quadrilatère AUVE est $\dfrac{5\sqrt{43}}{18}$.
1. On admet que le point U a pour coordonnées (0 ; 23 ; 1) .
Vérifier que le plan (EAU) a pour équation 3x−3y+5z−3=0 .
Montrez que les coordonnées des trois points du plan vérifissent bien l'équation...
Il suffit de s'assurer que les points A , E et U vérifient bien l'équation proposée.
Pour le point A , on a bien 3×1−3×0+5×0−3=0 .
De même pour le point E , il est clair que 3×0−3×(−1)+5×0−3=0 .
Et enfin, pour le point U , on vérifie mentalement que 3×0−3×23+5×1−3=0 .
Cette équation de plan convient donc.
Calculer l'équation d'un plan
- Définir un plan
Avant de calculer l'équation d'un plan, il faut le définir. Pour cela, on doit, à partir de trois points A,B,C du plan, montrer que les vecteurs \(\vec{AB}\) et \(\vec{AC}\) sont non colinéaires.
- Equation paramétrique de plan
Démonstration :
Soit les points A(xo;yo;zo) et M(x;y;z) et les vecteurs \(\vec{AB}\) (a;b;c) et \(\vec{AC}\) (a';b';c')
Si M est sur le plan $(A;\vec{AB};\vec{AC})$ alors le vecteur $\vec{MA}$ peut s'exprimer en fonction de $\vec{AB}$ et $\vec{AC}$
\(\vec{MA}\) $= (x_M - x_A; y_M - y_A ; z_M - z_A) = (x - x_o ; y - y_o ; z - z_o)$
x (\(\vec{MA}\) ) = ka + k'a' donc x - xo = ka + k'a' et x = ka + k'a' + xo
De même pour y et z
Formules :
Si on connait deux vecteurs non colinéaires d'un plan \(\vec{u}\)(a;b;c) et \(\vec{v}\) (a';b';c') et le point $A (x_o;y_o;y_o)$ apartenant au plan, alors une équation paramétrique de ce plan est :
$\begin{cases} x = ka + k'a' + xo\\ y = kb + k'b' + yo\\ z = kc + k'c' + zo \end{cases}$
avec k et k' des réels.
Exemple :
Soit A (-1;2;3), \(\vec{u}\)(4;-5;7) et \(\vec{v}\) (2;-1;8)
Une équation paramétrique de ce plan est :
$\begin{cases} x=4k+2k'-1\\y=-5k-k'+2\\z=7k+8k'+3 \end{cases}$
avec k et k' des réels
- Equation cartésienne de plan
Soit \(\vec{n}\) (a;b;c) un vecteur normal au plan (ABC) et d réel
Alors une équation cartésienne du plan (ABC) est ax + by + cz + d = 0
Exemple :
On connait le vecteur \(\vec{n}\) (1;7;5) normal au plan (BCD) et B (2;5;2)
Une équation cartésienne de (BCD) est x + 7y + 5z + d = 0
On cherche d : il faut remplacer les coordonnées d'un point appartenant au plan (ici le point B) dans l'équation:
2 + 7*5 + 5*2 + d = 0 donc 47 + d = 0 et d = -47
On obtient alors l'équation cartésienne du plan (BCD) : x + 7y + 5z -47 = 0
Remarques :
En éliminant les paramêtre $k$ et $k'$ on peut transformer un équation paramétrique en équation cartésienne.
Le contraire est possible en posant $x=k$ et $y=k'$ par exemple.
Astuce :
Pour savoir si deux équations correspondent au même plan, choisir trois points au hasard de la première et voir si les coordonnées vérifient la seconde.
2. Donner une représentation paramétrique de la droite $(d)$ orthogonale au plan $(EAU)$ passant par le point S.
Trouvez déjà l'équation cartésienne du plan $(EAU)$ grâce à un vecteur normal à ce plan...
Puis en s'aidant des coordonnées d'un point et d'un vecteur directeur appartenant tous deux au plann, déduisez-en une équation paramétrique...
Puisque l'on a muni l'espace d'un repère orthonormé, on déduit de l'équation cartésienne proposée les coordonnées d'un vecteur normal au plan $(EAU)$. Notons $\vec{n}$ (3 ; -3 ; 5) ce vecteur.
C'est un vecteur directeur de $(d)$ puisque $(d)$ est orthogonale au plan $(EAU)$. À partir des coordonnées du point $S$ et de celles de ce vecteur, on en déduit une équation paramétrique de $(d)$:
\[
\left \{
\begin{array}{lcl}
x & = & 3t\\
y & = & -3t\\
z & = & 3+5t
\end{array}
\right .
\quad t \, \in \, \mathbb{R}
\]
Calculer l'équation d'un plan
- Définir un plan
Avant de calculer l'équation d'un plan, il faut le définir. Pour cela, on doit, à partir de trois points A,B,C du plan, montrer que les vecteurs \(\vec{AB}\) et \(\vec{AC}\) sont non colinéaires.
- Equation paramétrique de plan
Démonstration :
Soit les points A(xo;yo;zo) et M(x;y;z) et les vecteurs \(\vec{AB}\) (a;b;c) et \(\vec{AC}\) (a';b';c')
Si M est sur le plan $(A;\vec{AB};\vec{AC})$ alors le vecteur $\vec{MA}$ peut s'exprimer en fonction de $\vec{AB}$ et $\vec{AC}$
\(\vec{MA}\) $= (x_M - x_A; y_M - y_A ; z_M - z_A) = (x - x_o ; y - y_o ; z - z_o)$
x (\(\vec{MA}\) ) = ka + k'a' donc x - xo = ka + k'a' et x = ka + k'a' + xo
De même pour y et z
Formules :
Si on connait deux vecteurs non colinéaires d'un plan \(\vec{u}\)(a;b;c) et \(\vec{v}\) (a';b';c') et le point $A (x_o;y_o;y_o)$ apartenant au plan, alors une équation paramétrique de ce plan est :
$\begin{cases} x = ka + k'a' + xo\\ y = kb + k'b' + yo\\ z = kc + k'c' + zo \end{cases}$
avec k et k' des réels.
Exemple :
Soit A (-1;2;3), \(\vec{u}\)(4;-5;7) et \(\vec{v}\) (2;-1;8)
Une équation paramétrique de ce plan est :
$\begin{cases} x=4k+2k'-1\\y=-5k-k'+2\\z=7k+8k'+3 \end{cases}$
avec k et k' des réels
- Equation cartésienne de plan
Soit \(\vec{n}\) (a;b;c) un vecteur normal au plan (ABC) et d réel
Alors une équation cartésienne du plan (ABC) est ax + by + cz + d = 0
Exemple :
On connait le vecteur \(\vec{n}\) (1;7;5) normal au plan (BCD) et B (2;5;2)
Une équation cartésienne de (BCD) est x + 7y + 5z + d = 0
On cherche d : il faut remplacer les coordonnées d'un point appartenant au plan (ici le point B) dans l'équation:
2 + 7*5 + 5*2 + d = 0 donc 47 + d = 0 et d = -47
On obtient alors l'équation cartésienne du plan (BCD) : x + 7y + 5z -47 = 0
Remarques :
En éliminant les paramêtre $k$ et $k'$ on peut transformer un équation paramétrique en équation cartésienne.
Le contraire est possible en posant $x=k$ et $y=k'$ par exemple.
Astuce :
Pour savoir si deux équations correspondent au même plan, choisir trois points au hasard de la première et voir si les coordonnées vérifient la seconde.
Calculer l'équation d'une droite
Définition
Une équation de droite dans l'espace peut s'écrire de deux façons :
-équation paramétrique de droite
-équation cartésienne de droite
On utilisera plus souvent l'équation paramétrique. Alors :
soit A un point dans l'espace de coordonnées ($x_{0} ; y_{0} ; z_{0}$), et $\vec{u} $ un vecteur non nul de coordonnées (a ; b ; c). Si d est la droite passant par A et $\vec{u}$, alors son équation paramétrique est
$\begin{cases} x = x_{0} + at\\ y = y_{0} + bt\\ z = z_{0} + ct avec t\in\mathbb{R} \end{cases}$
Remarque :
$t\in\mathbb{R}$ signifie qu'à chaque t correspond un point de la droite. Si on $t\in [-1;1]$ alors on à un segment. C'est donc un élément essentiel de l'équation.
Exemple :
Si une droite d passe par le point A de coordonnées (5 ; 2 ; 1) et par $\vec{u}$(2 ; 6 ; 10), alors son équation paramétrique est :
$\begin{cases} x = 5 + 2t\\ y = 2 + 6t\\ z = 1 + 10t avec t\in\mathbb{R} \end{cases}$
Complément :
Une équation cartésienne est de la forme
$\begin{cases} ax + by + cz + d =0\\ a'x + b'x + c'x + d'=0 \end{cases}$
Cela correspond à l'intersection de deux plans.
Comme une droite peut être à l'intersection de beaucoup de plans différents, il existe une infinité d'équation cartésienne trés différentes pour une même droite.
Astuce :
Pour savoir si deux équations corespondent à la même droite, il suffit de choisir au hasard deux points de l'une et tester s'ils sont sur l'autre !
3. Déterminer les coordonnées de H, point d'intersection de la droite $(d)$ et du plan $(EAU)$.
Rappellez-vous que si un point appartient à la fois à une droite et à un plan, alors ses coordonnées vériffissent les deux équations...
Trouvez donc le bon paramètre $t$ tel que $H$ soit élément de $(d)$ et $(EAU)$...
Les coordonnées ($x$ ; $y$ ; $z$) de ce point satisfont simultanément une équation paramétrique de $(d)$ ainsi qu'une équation cartésienne du plan $(EAU)$. On cherche donc $x$, $y$, $z$ et $t$ tels que:
\[
\left \{
\begin{array}{lcl}
x & = & 3t\\
y & = & -3t\\
z & = & 3+5t\\
0 & = & 3x-3y+5z-3
\end{array}
\right .
\]
À partir de l'équation cartésienne du plan, en substituant $x$, $y$ et $z$ on en déduit le système équivalent:
\[
\left \{
\begin{array}{lcl}
x & = & 3t\\
y & = & -3t\\
z & = & 3+5t\\
0 &= & 3(3t)-3(-3t)+5(3+5t)-3
\end{array}
\right .
\]
La dernière équation permet de déterminer $t = \dfrac{-12}{43}$ et, par suite, on peut déterminer les coordonnées de $H$ (${\frac{-36}{43}} ; {\frac{36}{43}} ; {\frac{69}{43}}$).
Trouver une intersection
Il y a plusieurs types d'intersections:
Intersection de deux droites:
Si deux droites sont coplanaires et non parallèles alors leur intersection est un point.

Pour trouver les coordonnées du point d'intersection entre la droite D et la droite D', il faut se servir des équations paramétriques les deux droites et résoudre le système.
On cherche un couple de paramêtre $k$ et $k'$ tel que les valeurs de $x,y,z$ soient les même pour les deux droites.
Intersection d'une droite et d'un plan:
L'intersection entre une droite et un plan est un point
.png)
Pour trouver les coordonnées du point d'intersection entre la droite D et la plan P, il faut une équation cartésienne du plan et une équation paramétrique du plan. On remplace les x, y et z dans l'éqution du plan jusqu'à obtenir une valeur de t. On remplace cette valeur dans l'équation paramétrique de la droite D et on résout pour trouver des valeurs de x, y et z qui correspondent aux coordonnées du point d'intersection entre la droite D et la plan P.
Intersection de deux plans:
Si les deux plans ne sont pas parallèles, l'intersection entre deux plans est une droite.

Le système constitué par ces deux équations est un système d'équation cartésienne de droite.
On peut trouver un système d'équation paramètrique de la droite en posant $x=k$ ou $y=k$ ou ...
Remarque : Si un point appartient aux deux plans, il appartient à la droite d'intersection, et deux points définissent une droite.
Intersection d'un plan et d'une sphère:
L'intersection entre un plan et une sphère est un cercle.

Remarque : Le centre du cercle, celui de la sphère et un point du cercle forment un triangle rectangle, penser à Pythagore
Remarque : La distance entre le centre de la sphère et le plan donne la nature de l'intersection (vide, point ou cercle )
4. Le plan (EAU) partage la pyramide (SABCE) en deux solides. Ces deux solides ont-ils le même volume ?
Aidez vous de toutes les questions précédentes pour calculer l'aire du tétraèdre $SABCE$...
Puis, comparez le à la moitié du volume du solide entier...
Le plan $(EAU)$ coupe le tétraèdre $SABCE$ en un prisme $ABUECV$ d'une part et un tétraèdre $SAUVE$ d'autre part. Il nous faut donc déterminer si ces deux solides ont le même volume; ce qui revient à déterminer si le volume de l'un des deux solides correspond à la moitié de celui de $SABCE$.
Or toutes les questions précédentes nous ont permis de rassembler des éléments permettant de calculer le volume du tétraèdre $SAUVE$. Nous connaissons en effet l'aire de sa base $\mathcal{A}_{AUVE} = \dfrac{5\sqrt{43}}{18}$. Reste à calculer sa hauteur $SH$. On a ainsi:
\begin{align*}
SH & = \sqrt{\left(\dfrac{-36}{43}-0\right)^2+\left(\dfrac{36}{43}-0\right)^2+\left(3-\dfrac{69}{43}\right)^2} \\
& = \dfrac{12}{\sqrt{43}}
\end{align*}
Le volume du tétraèdre $SAUVE$ est donc $\mathcal{V}_{SAUVE} = \dfrac{1}{3}\mathcal{A}_{AUVE} \times SH $, ce qui donne après calcul: $\mathcal{V}_{SAUVE} = \dfrac{10}{9}$.
Pour finir, déterminons le volume de la grande pyramide $SABCE$. On peut, par application du théorème de Pythagore au triangle $ABO$ rectangle en $O$ prouver que $AB = \sqrt{2}$. Sa base a donc pour aire $AB^2=2$. D'autre part, sa hauteur est $SO=3$. Le volume de la grosse pyramide est donc $\mathcal{V}_{SABCE} = \dfrac{1}{3} AB^2 \times SO = 2$.
On constate que $\dfrac{1}{2} \mathcal{V}_{SABCE} \neq \mathcal{V}_{SAUVE}$, ce qui permet de conclure.
Calculer un volume
Le volume d'un tétraèdre se calcule grâce à la formule:
\[\mathcal{V}=\dfrac13\times h\times Base\]
-La "Base" est l'aire du triangle.
-h étant la hauteur du tétraèdre, la hauteur est la droite orthogonale au plan de la base passant par le sommet opposé.

Méthode:
Pour calculer la hauteur d'un tétraèdre:
-commencer par déterminer l'équation cartésienne du plan de la base et la représentation paramétrique de la hauteur
-remplacer l'équation cartésienne du plan dans la représentation paramétrique de h pour déterminer la valeur de t
-pour déterminer les coordonnées de l'intersection du plan et de la hauteur que l'on appellera B, il faut remplacer t dans l'équation cartésienne du plan de la base
-calculer la distance entre le sommet opposé à la base et B
Remarques:
Le volume d'un tétraèdre peut se calculer de 4 façons différentes car il possède 4 faces donc 4 possibles bases et leur hauteur.
Si on calcule le volume d'un tétraèdre, on peut en déduire la distance d'une autre hauteur.
Formules:
Volume d'un cube:
\(V=a^3\)
"a" est la longueur d'une arrète.
Volume d'un parallélépipède rectangle:
\(V=l L h\)
"l" est la largeur,"L" est la longueur et "h" est la hauteur.
Volume d'une sphère:
\(V=\frac{4}{3}\pi r^3\)
"r" étant le rayon de la sphère.
Volume d'un cylindre:
\(V=\pi r^2 h\) 
"r" étant le rayon et "h" la hauteur
.JPG)


