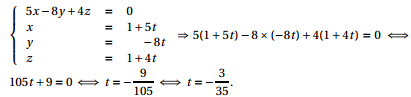Soit un cube ABCDEFGH d'arête 1.
Dans le repère $\left(\text{A};\vec{AB},\vec{AD},\vec{AE}\right)$, on considère les points M, N et P de coordonnées
respectives M$\left(1~;~1~;~\dfrac{3}{4}\right)$, N$\left(0~;~\dfrac{1}{2}~;~1\right)$, P$\left(1~;~0~;~- \dfrac{5}{4}\right)$.
1) Déterminer les coordonnées des vecteurs $\vec{MN}$ et $\vec{MP}$.
En déduire que les points M, N et P ne sont pas alignés.
2) On considère l'algorithme 1.
a) Exécuter à la main cet algorithme avec les coordonnées des points M, N et P
données ci-dessus.
b) À quoi correspond le résultat affiché par l'algorithme ? Qu'en déduire pour le
triangle MNP ?
3) On considère l'algorithme 2
Le compléter pour qu'il teste et affiche si un triangle MNP est rectangle et isocèle en M.
4) On considère le vecteur $\vec{n}(5~;- 8~;~4)$ normal au plan (MNP).
a) Déterminer une équation cartésienne du plan (MNP).
b) On considère la droite $\Delta$ passant par F et de vecteur directeur $\vec{n}$.
Déterminer une représentation paramétrique de la droite $\Delta$.
5) Soit K le point d'intersection du plan (MNP) et de la droite $\Delta$.
a) Démontrer que les coordonnées du point K sont $\left(\dfrac{4}{7}~;~\dfrac{24}{35}~;~\dfrac{23}{35}\right)$.
b) On donne FK $= \sqrt{\dfrac{27}{35}}$.
Calculer le volume du tétraèdre MNPF.