Page

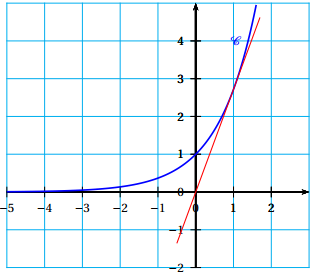
On considère la courbe $\mathcal{C}$ d'équation $y = \text{e}^x$, tracée ci-dessous.

Pour tout réel $m$ strictement positif, on note $\mathcal{D}_m$ la droite d'équation $y = mx$.

Dans cette question, on choisit $m = \text{e}$.

1. Démontrer que la droite $\mathcal{D}_{\text{e}}$, d'équation $y = \text{e}x$, est tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1.

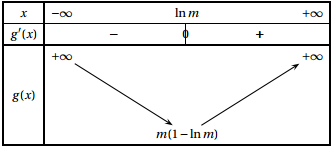
2. Conjecturer, selon les valeurs prises par le réel strictement positif $m$, le nombre de
points d'intersection de la courbe $\mathcal{C}$ et de la droite $\mathcal{D}_m$.

3. Démontrer cette conjecture.

Première solution
Le point M de coordonnées $(x,~y)$ est un point d'intersection de $\mathcal{C}$ et de $\mathcal{D}_m$ si et seulement si
\[\mathrm{e}^x=mx\iff \mathrm{e}^x-mx=0.\]

Posons $f(x) = \mathrm{e}^x - mx$, alors

\[\mathrm{e}^x=mx\iff f(x)=0.\]

Étudions cette fonction $f$, il vient:

$f'(x)=\mathrm{e}^x-m$

$\displaystyle{\lim_{x\to -\infty}f(x) = +\infty}$ car $\displaystyle{\lim_{x\to -\infty}\mathrm{e}^x=0}$ et $\displaystyle{\lim_{x\to -\infty}-mx=+\infty}$ car $m>0$

$f(x)=x\left(\dfrac{\mathrm{e}^x}{x}- m \right)$, or $\displaystyle{\lim_{x\to +\infty}\dfrac{\mathrm{e}^x}{x} = +\infty}$, donc

$\displaystyle{\lim_{x\to +\infty}f(x) = +\infty}$

$f'(x)>0\iff\mathrm{e}^x > m\iff x>\ln(m)$

$f\left(\ln(m)\right)=m-m\ln(m) = m\left(1-\ln(m)\right)$

D'où le tableau de variations

Il résulte de ce tableau de variations que

si $m(1 - \ln(m)) > 0$ alors l'équation $f(x) = 0$ n'admet pas de solution;
si $m(1 - \ln(m)) = 0$ alors l'équation $f(x) = 0$ admet une seule solution;
si $m(1 - \ln(m)) < 0$ alors l'équation $f(x) = 0$ admet deux solutions

Or comme $m > 0$,

\[m(1-\ln(m))>0\iff 1-\ln(m)>0\iff 1>\ln(m)\iff \mathrm{e}>m,\]

d'où, en définitive

si $m<\mathrm{e}$ alors la courbe $\mathcal{C}$ et la droite $\mathcal{D}_m$ n'auront aucun point d'intersection;
si $m=\mathrm{e}$ alors la courbe $\mathcal{C}$ et la droite $\mathcal{D}_m$ auront un seul point d'intersection;
si $m>\mathrm{e}$ alors la courbe $\mathcal{C}$ et la droite $\mathcal{D}_m$ auront deux points d'intersection.

Deuxième solution

On veut déterminer dans $\mathbb{R}$ le nombre de solutions de l'équation $e^x = mx$. On sait que $m>0$ et que, pour tout $x$, $e^x>0$ donc les solutions de cette équation seront strictement positives.

Sur $\mathbb{R}*$ , $e^x = mx \frac{e^x}{x} = m$.

Soit $f$ la fonction définie sur $\mathbb{R}*$ par $f(x)=\frac{e^x}{x}$.

Cette fonction est dérivable comme quotient de fonctions dérivables et:

$f'(x) = \frac{xe^x-e^x}{x^2} = \frac{e^x(x-1)}{x^2}$

Le signe de $f'(x)$ est le même que le signe de $x-1$ donc négatif sur $]0\,,\,1[$ puis positif sur $]1\,,\,+\infty[$. La fonction $f$ admet donc un minimum pour $x=1$ égal à $f(1)=\frac{e^1}{1}=e$.

D'après le cours, $\lim_{x \to +\infty} \frac{e^x}{x}=+\infty$.

$\lim_{x\to 0}e^x=1$
$\lim_{x\to 0 \atop x>0} \frac{e^x}{x}=+\infty$

On établit le tableau de variation de la fonction $f$:

Déterminer le nombre de solutions $f(x)=m$ revient à déterminer le nombre de points d'intersection de la courbe $\mathcal C_f$ représentant la fonction $f$ et de la droite horizontale $\mathcal D$ d'équation $y=m$.

D'après le tableau de variation de $f$:

si $m<e$, la courbe $\mathcal C_f$ et la droite $\mathcal D$ n'ont pas de point d'intersection donc la droite $\mathcal D_m$ et la courbe $\mathcal C$ n'ont pas de point d'intersection;

si $m=e$, la droite $\mathcal D$ est tangente à la courbe $\mathcal C_f$, donc $\mathcal D$ et $\mathcal C_f$ ont un seul point d'intersection, et donc la droite $\mathcal D_m$ et la courbe $\mathcal C$ ont un seul point d'intersection;

si $m>e$, la droite $\mathcal D$ et la courbe $\mathcal C_f$ ont deux points d'intersection, donc la droite $\mathcal D_m$ et la courbe $\mathcal C$ ont deux points d'intersection.