0 / 10 : Type Bac sur les fonctions 1.1 : Etude de fonctions ---- Dérivées

Une fonction f est dérivable en a si $\lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h}$

Lorsque h tend vers 0, $\frac{f(a+h)-f(a)}{h}$ se rapproche d'un nombre qui est la dérivée pour $x=a$.
Ici, la fonction représentée par la courbe est la fonction $f(x)=\frac{1}{4}x²+1$.


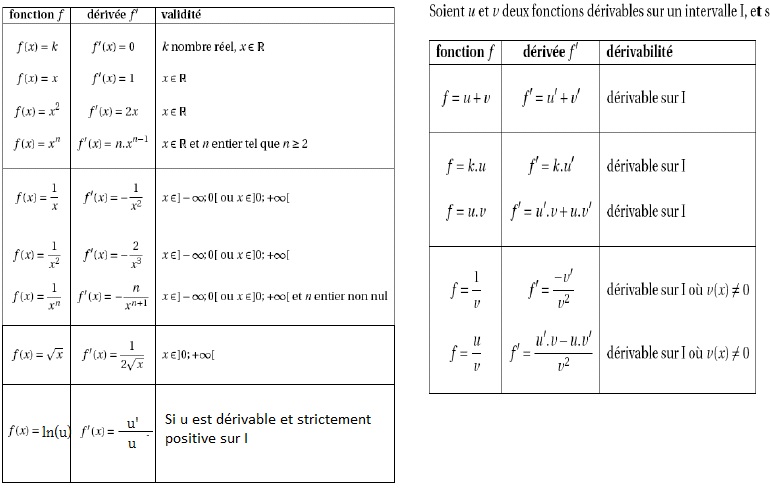
Voici pour vous aider un tableau récapitulatif des principales fonctions et de leurs dérivées :

Calculer la dérivée de la fonction $\frac{2x²+5}{x-2}$.