Le problème de Diffie-Hellman (abrégé DHP de l'anglais Diffie-Hellman problem)
est un problème mathématique évoqué en premier par Whitfield Diffie et Martin Hellman en cryptologie. Le leitmotiv de ce problème est le fait que beaucoup de systèmes de sécurité utilisent des opérations mathématiques rapides à calculer, mais très difficiles, voire impossibles à l'échelle humaine, à inverser. Par exemple il est facile de calculer le hash d'un message avec les fonctions mathématiques de hachage, mais très difficile de revenir au message originel. Si la résolution du problème de Diffie-Hellman était facile, ces systèmes seraient faciles à corrompre.
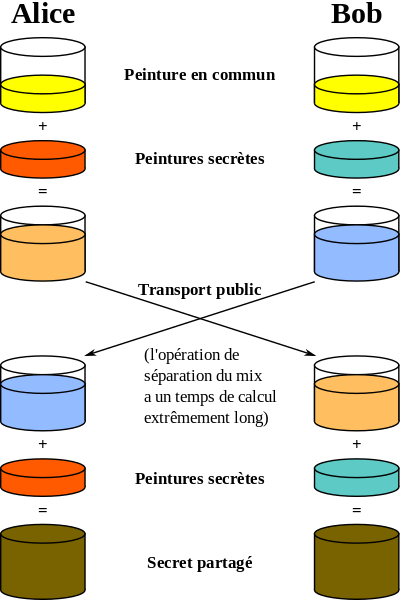
Parallèlement à leur découverte du principe de la cryptographie à clé publique, Diffie et Hellman ont proposé en 1976 un protocole d'échange de clés totalement sécurisé. Le problème est le suivant. Alice et Bob veulent s'échanger un message crypté en utilisant un algorithme nécessitant une clé K. Ils veulent s'échanger cette clé K, mais ils ne disposent pas de canal sécurisé pour cela. Le protocole d'échange de clés de Diffie et Hellman répond à ce problème lorsque K est un nombre entier. Il repose sur l'arithmétique modulaire, et sur le postulat suivant :
